This post originally appeared at scientificamerican.com.
On our most recent episode of My Favorite Theorem, my cohost Kevin Knudson and I talked with University of Montreal math professor Matilde Lalín about her favorite bit of math, the congruent number problem. (You can listen to the episode or read a transcript at kpknudson.com.)
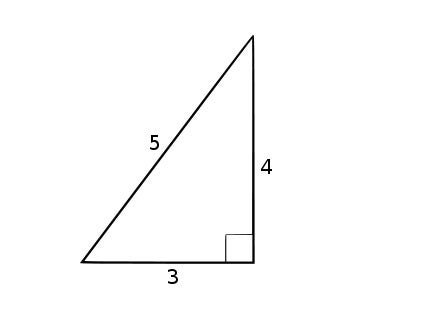
A congruent number is a positive whole number that can be the area of a right triangle with rational side lengths. So the number 6, for example, is a congruent number because it is the area of a 3-4-5 right triangle. The congruent number problem is to figure out what positive whole numbers are congruent numbers.
When I heard the term congruent number, my first question was, “Congruent to what?” But even though there are triangles involved, the name doesn’t come from the idea of two figures being congruent but from the Latin word congruum. Fibonacci used the term, which means something like “agreeing” or “harmonious,” to refer to the differences of squares in arithmetic progressions.
An arithmetic progression is a sequence of numbers with the same differences between successive numbers: 1, 3, 5, 7 is an arithmetic progression with difference 2, for example. Successive square numbers (1, 4, 9, 16, and so on) do not form an arithmetic progression, but if you skip some, you can find a set of squares that have that relationship to each other. The squares 1, 25, and 49 all have difference 24, so Fibonacci would have called 24 a congruum.
My first question answered, my natural second question: What do congruent numbers and congrua have to do with each other? How do we get from arithmetic progressions to triangles? There are early hints at congrua and congruent numbers in the work of 3rd century CE mathematician Diophantus of Alexandria, but the topic is raised more explicitly in 10th century Arab manuscripts, including one by Mohammed Ben Alhochain, who wrote that the principal object of study in the subject of rational right triangles is finding congrua.
It’s no coincidence that my first example of a congruent number is 6 and my first example of a congruum is 24. By knowing that 24 is a congruum, we can construct the triangle with rational side lengths and area 6.
The congruum in our first example is 24, and the three squares in arithmetic progression are 12, 52, and 72. Early mathematicians recognized that when three squares occurred in arithmetic progression this way, the square root of the middle number — in this case, 5 — is the hypotenuse of the right triangle. The sum of the lengths of the two legs is the square root of the largest number, and the difference of their lengths is the larger number. If two numbers add up to 7 and have a difference of 1, a simple system of equations shows that the numbers are 3 and 4. The area of the triangle, then, is 6, a quarter of the congruum 24.
That idea works in general. Any sequence of squares x2, y2, z2 with common difference k has the property that k is 4 times the area of the right triangle with hypotenuse length y and leg lengths a and b, where a and b are determined by the two equations a+b=z and a-b=x. It seems a little overwhelming to see all at once, but it’s not too hard to verify for yourself if you feel like pushing some symbols around.
As Dr. Lalín told us, mathematicians have been trying to find criteria for determining whether a given number is a congruent number for a long time. Some facts are known: no squares are congruent numbers; if a prime number is 3 more than a multiple of 8, it is not congruent, but its double is; every congruent number is a congruum multiplied by a square of a rational number. That last one might seem like a jackpot, but there are a lot of squares of rational numbers, and it’s not easy to see whether a given rational number times a congruum will yield a congruent number. One of the consequences of the Birch and Swinnerton-Dyer conjecture, considered to be one of the most important unsolved problems in mathematics, is that there is an easy procedure to determine whether a given number is congruent.
For more information on congruent numbers, congrua, and the Birch and Swinnerton-Dyer conjecture, check out the show notes for our episode of My Favorite Theorem with Matilde Lalín or History of the Theory of Numbers Volume II by Leonard Eugene Dickson. (The section on congruent numbers begins on page 459 of the linked book.) You can find a list of a lot of congruent numbers at the Online Encyclopedia of Integer Sequences.


Recent Comments